¿Qué es la distribución normal? ¿tiene fórmula? ¿cómo se representa? ¿se podría reconocer fácilmente? Sobre todo esto y mucho más vamos a hablar en esta entrada.
Definición de distribución normal
La distribución normal es un modelo teórico capaz de aproximar satisfactoriamente el valor de una variable aleatoria a una situación ideal. Es, además, la base de otras distribuciones como: la distribución t de Student, distribución ji-cuadrada y la distribución F de Fisher, entre otras. Se representa con una fórmula en la que se conjugan la media o mediana y la desviación típica. Esta fórmula tiene en cuenta una variable aleatoria.
La fórmula de la distribución normal
Dada una variable aleatoria X, decimos que la frecuencia de sus observaciones puede aproximarse satisfactoriamente a una distribución normal tal que:




Representación gráfica de la distribución normal
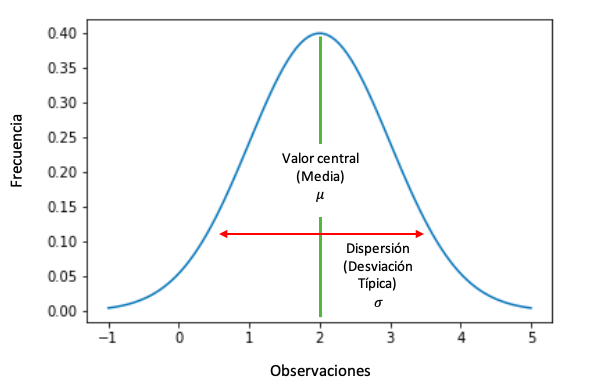
Gráficamente, es una función de densidad de una variable aleatoria que sigue una distribución normal.

Propiedades de la distribución normal
- Es una distribución simétrica, ya que el valor de la media, la mediana y la moda coinciden. Es decir:
Media = Mediana = Moda
- Es una distribución unimodal. Los valores que son más frecuentes o que tienen más probabilidad de aparecer están alrededor de la media. En otras palabras, cuando nos alejamos de la media, la probabilidad de aparición de los valores y su frecuencia descienden.
Datos que necesitas para poder establecer una distribución normal
Hay determinada información que es necesaria si queremos establecer una distribución normal. Para ello necesitarás disponer de:
- Una Variable Aleatoria.
- La media calculada.
- La desviación típica calculada.
- Decidir la función que queremos representar: función de densidad de probabilidad o función de distribución.
Ejemplo práctico para entender una distribución normal
Somos profes de secundaria y queremos saber si los resultados de los exámenes de nuestros alumnos poddrían aproximarse satisfactoriamente a una distribución. ¿Qué podemos hacer? Pues, vamos a ver si disponemos de todos los ingredientes para poder responder a la pregunta.
Bien, para empezar, Sabemos que el examen lo han realizado 475 estudiantes y que los resultados pueden oscilar desde un 0 hasta el 10. Teniendo los resultados de los exámenes, deberemos calcular dos valores a partir de estas observaciones (los valores de los resultados obtenidos). También definiremos la Variable Aleatoria x como los resultados del examen que depende de cada resultado individual.


Entonces…
- Calculamos la media
- Calculamos la desviación típica.
- Definimos variable aleatoria como «resultados del examen».
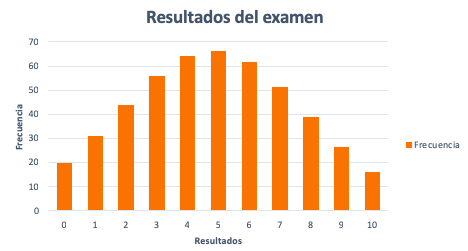
Vamos a ordenar la información relevante en una tabla:
| Resultados | Frecuencia |
|---|---|
| 0 | 20 |
| 1 | 31 |
| 2 | 44 |
| 3 | 56 |
| 4 | 64 |
| 5 | 66 |
| 6 | 62 |
| 7 | 51 |
| 8 | 39 |
| 9 | 26 |
| 10 | 16 |
| TOTAL | 475 |
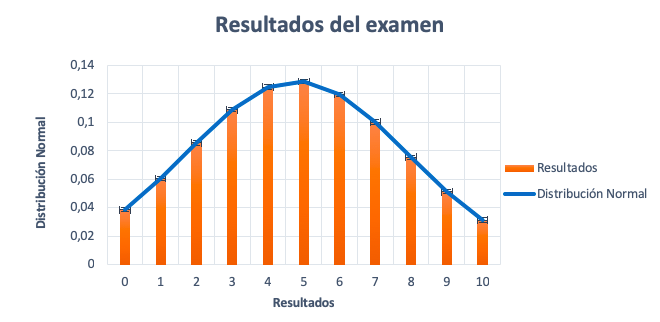
A continuación, pasamos a representar los resultados en forma de gráfico, concretamente, en un histograma. Queremos distribuir los resultados gráficamente, para comprobar cómo se reparte densidad de cada resultado (frecuencia) en dicha gráfica y poder valorar si podría «encajar» en un gráfico de distribución normal o no.

El gráfico se parece a la imagen anterior y cumple con las propiedades, entonces, la variable resultados del examen puede aproximarse satisfactoriamente a una distribución normal de media 4,86 y desviación típica de 2,56. Mira:
μ = (0.042×0+0.065×1+0.093×2+0.118×3+0.135×4+0.139×5+0.131×6+0.107×7+0.082×8+0.055×9+0.034×10) / (0.042+0.065+0.093+0.118+0.135+0.139+0.131+0.107+0.082+0.055+0.034) = 4.86113886 σ = √( (0.042×(0-4.86113886)²+0.065×(1-4.86113886)²+0.093×(2-4.86113886)²+0.118×(3-4.86113886)²+0.135×(4-4.86113886)²+0.139×(5-4.86113886)²+0.131×(6-4.86113886)²+0.107×(7-4.86113886)²+0.082×(8-4.86113886)²+0.055×(9-4.86113886)²+0.034×(10-4.86113886)²) / (0.042+0.065+0.093+0.118+0.135+0.139+0.131+0.107+0.082+0.055+0.034) ) = 2.55639651
Dicho todo lo anterior, ¿podemos asegurar que los resultados del examen se aproximen a una distribución normal, según las propiedades estudiadas para este tipo de distribución? o, en otras palabras, ¿existen razones para considerar que la variable de resultados sigue una distribución normal?
| Pregunta | Respuesta | Justificación |
|---|---|---|
| ¿Es una distribución simétrica? | Sí | Hay mismsa cantidad de observaciones tanto a la derecha como a la izquierda del valor central. También, que la media, la mediana y la moda tienen el mismo valor. |
| ¿Media = Mediana = Moda? | Sí | Media = Mediana = Moda = 5 |
| ¿Distribución unimodal? | Sí | Las observaciones con más frecuencia o probabilidad están alrededor del valor central. En otras palabras, las observaciones con menos frecuencia o probabilidad se encuentran lejos del valor central. |


La variable resultados del examen sigue una distribución normal.
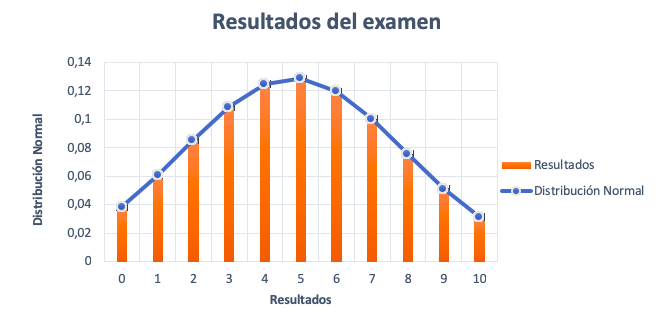

La distribución normal describe la variable aleatoria mediante una aproximación que produce errores estándar (las barras encima de cada columna). Estos errores son la diferencia entre las observaciones reales (resultados) y la función de densidad (distribución normal).